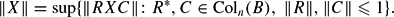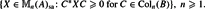Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
CAMERON, JAN M.
2011.
STRUCTURE RESULTS FOR NORMALIZERS OF II1 FACTORS.
International Journal of Mathematics,
Vol. 22,
Issue. 07,
p.
947.
Cameron, Jan
and
Smith, Roger R.
2015.
Bimodules in crossed products of von Neumann algebras.
Advances in Mathematics,
Vol. 274,
Issue. ,
p.
539.
Cameron, Jan M.
and
Smith, Roger R.
2016.
Intermediate subalgebras and bimodules for general crossed products of von Neumann algebras.
International Journal of Mathematics,
Vol. 27,
Issue. 11,
p.
1650091.
Lin, Ying-Fen
and
Todorov, Ivan G
2021.
Operator System Structures and Extensions of Schur Multipliers.
International Mathematics Research Notices,
Vol. 2021,
Issue. 17,
p.
12809.
Pitts, David R.
Smith, Roger R.
and
Zarikian, Vrej
2024.
Norming in discrete crossed products.
Illinois Journal of Mathematics,
Vol. 68,
Issue. 4,


 (
(