Completeness properties in L2 of the eigenfunctions of two semi-linear differential operators
Published online by Cambridge University Press: 24 October 2008
Extract
This paper concerns the boundary-value problems
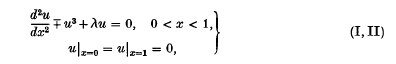
in which λ is a real parameter, u is to be a real-valued function in C2[0, 1], and problem (I) is that with the minus sign. (The differential operators 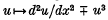 are called semi-linear because the non-linearity is only in undifferentiated terms.) If we linearize the equations (for ‘ small’ solutions u) by neglecting
are called semi-linear because the non-linearity is only in undifferentiated terms.) If we linearize the equations (for ‘ small’ solutions u) by neglecting 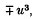 , there result the eigenvalues λ = n2π2 (with n = 1,2,…) and corresponding normalized eigenfunctions
, there result the eigenvalues λ = n2π2 (with n = 1,2,…) and corresponding normalized eigenfunctions

and it is well known ((2), p. 186) that the sequence {en} is complete in that it is an orthonormal basis for the real Hilbert space L2(0, 1). We shall be concerned with possible extensions of this result to the non-linear problems (I) and (II), for which non-trivial solutions (λ, u) bifurcate from the trivial solution (λ, 0) at the points {n2π2,0) in the product space 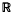 × L2(0, 1). (Here
× L2(0, 1). (Here 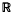 denotes the real line.)
denotes the real line.)
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 3 , November 1980 , pp. 451 - 468
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
- 3
- Cited by


