Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T11:34:15.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely 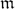${\mathfrak m}$-full ideals and componentwise linear ideals

Published online by Cambridge University Press:  10 December 2014

TADAHITO HARIMA  and
JUNZO WATANABE
TADAHITO HARIMA
Affiliation:
Department of Mathematics Education, Niigata University, Niigata 950-2181, Japan. e-mail: [email protected]
JUNZO WATANABE
Affiliation:
Department of Mathematics, Tokai University, Hiratsuka 259-1292, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the class of completely 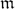${\mathfrak m}$-full ideals coincides with the class of componentwise linear ideals in a polynomial ring over an infinite field.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 2 , March 2015 , pp. 239 - 248
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Conca, A.Reduction number and initial ideals. Proc. Amer. Math. Soc. 131 (2003), 1015–1020.CrossRefGoogle Scholar
[2]Goto, S.Integral closedness of complete-intersection ideals. J. Algebra. 108 (1987), 151–160.CrossRefGoogle Scholar
[3]Goto, S. and Hayasaka, F.Finite homological dimension and primes associated to integrally closed ideals. Proc. Amer. Math. Soc. 130 (2002) 3159–3164.CrossRefGoogle Scholar
[4]Green, M. L.Generic initial ideals. Six Lectures on Commutative Algebra. Birkhäuser Verlag, Basel. Prog. Math. 166 (1998), 119–186.CrossRefGoogle Scholar
[5]Herzog, J. and Hibi, T.Componentwise linear ideals. Nagoya Math. J. 153 (1999), 141–153.CrossRefGoogle Scholar
[6]Harima, T. and Watanabe, J.The weak Lefschetz property for ${\mathfrak m}$-full ideals and componentwise linear ideals. Illinois J. Math. 156 (2012), 957–966.Google Scholar
[7]Nagel, U. and Römer, T.Criteria for componentwise linearity. Commun. Algebra. 43 (2015), 1–18.CrossRefGoogle Scholar
[8]Watanabe, J.${\mathfrak m}$-full ideals. Nagoya Math. J. 106 (1987), 101–111.CrossRefGoogle Scholar
[9]Watanabe, J.The syzygies of ${\mathfrak m}$-full ideals. Math. Proc. Camb. Phil. Soc. 109 (1991), 7–13.CrossRefGoogle Scholar
[10]Watanabe, J.${\mathfrak m}$-full ideals II. Math. Proc. Camb. Phil. Soc. 111 (1992), 231–240.CrossRefGoogle Scholar