No CrossRef data available.
Published online by Cambridge University Press: 08 April 2016
By considering the Bredon analogue of complete cohomology of a group, we show that every group in the class 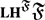 $\cll\clh^{\mathfrak F}{\mathfrak F}$ of type Bredon-FP∞ admits a finite dimensional model for
$\cll\clh^{\mathfrak F}{\mathfrak F}$ of type Bredon-FP∞ admits a finite dimensional model for  $E_{\frak F}G$.
$E_{\frak F}G$.
We also show that abelian-by-infinite cyclic groups admit a 3-dimensional model for the classifying space for the family of virtually nilpotent subgroups. This allows us to prove that for 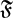 $\mathfrak {F}$, the class of virtually cyclic groups, the class of
$\mathfrak {F}$, the class of virtually cyclic groups, the class of 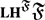 $\cll\clh^{\mathfrak F}{\mathfrak F}$-groups contains all locally virtually soluble groups and all linear groups over
$\cll\clh^{\mathfrak F}{\mathfrak F}$-groups contains all locally virtually soluble groups and all linear groups over 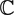 ${\mathbb{C}}$ of integral characteristic.
${\mathbb{C}}$ of integral characteristic.