Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T08:33:50.835Z Has data issue: false hasContentIssue false
  • English
  • Français

The cohomology of finite H-spaces as U(M) algebras. II

Published online by Cambridge University Press:  24 October 2008

Richard Kane
Richard Kane
Affiliation:
University of Western Ontario, London, Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a continuation of (6). We will use the definitions and notation of (6) freely. We continue our study of the restrictions imposed on the mod p cohomology of finite H-spaces by the requirement that 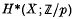is a U(M) algebra. As in (6) we will restrict our attention to the case where p is an odd prime. As we observed in (6), the restriction proved there, that the pth power map on 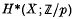is trivial, may not really require the hypothesis of 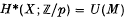. However, the restrictions proved in this paper are not valid without the assumption that 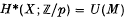. Indeed, they actually characterize the known mod odd finite H-spaces which have U(M) algebras.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 1 , July 1981 , pp. 113 - 125
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Browder, W.Torsion in H-spaces. Annals of Math. 74 (1961), 24–51.CrossRefGoogle Scholar
(2)Harper, J. R.H-spaces with torsion. Amer. Math. Soc. Mem. 223 (1979).Google Scholar
(3)Johnson, D. C. and Wilson, W. S.Protective dimension and Brown-Peterson homology. Topology 12 (1973), 327–353.CrossRefGoogle Scholar
(4)Kane, R.The module of indecomposables for finite H-spaces. Trans. Amer. Math. Soc. 222 (1976), 303–318.Google Scholar
(5)Kane, R.Brown-Peterson operations and Steenrod modules. Quart. J. Math. Oxford 30 (1979), 455–567.CrossRefGoogle Scholar
(6)Kane, R.The cohomology of finite H-spaces as U(M) algebras: I. Math. Proc. Cambridge Philos. Soc. 89 (1981), 473–490.CrossRefGoogle Scholar
(7)Lin, J.Torsion in H-spaces: II. Annals of Math. 107 (1978), 41–88.CrossRefGoogle Scholar
(8)Milnor, J.The Steenrod algebra and its dual. Annals of Math. 67 (1958), 150–171.CrossRefGoogle Scholar
(9)Milnor, J. and Moore, J. C.On the structure of Hopf algebras. Annals of Math. 81 (1965), 211–264.CrossRefGoogle Scholar
(10)Yagita, N. On mod odd prime Brown-Peterson cohomology subgroups of exceptional Lie groups. (To appear.)Google Scholar
(11)Yagita, N. The BP*-module structure of BP*(E 8) (or p) = 3. (To appear.)Google Scholar
(12)Zabrodsky, A.Implications in the cohomology of H-spaces. Ill. J.Math. 14 (1970), 363–375.Google Scholar