Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-06T01:05:57.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent groups of units of integral group rings and direct products of free groups

Published online by Cambridge University Press:  28 June 2016

ÁNGEL DEL RÍO  and
PAVEL ZALESSKII
ÁNGEL DEL RÍO
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, 30100, Murcia, Spain. e-mail: [email protected]
PAVEL ZALESSKII
Affiliation:
Departamento de Matemática, Universidade de Brasília, 70.910-900, Brasilia-DF, Brasil. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We classify the finite groups G for which 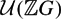$\mathcal{U}({\mathbb Z} G)$, the group of units of the integral group ring of G, does not contain a direct product of two non-abelian free groups. This list of groups contains all the groups for which 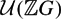$\mathcal{U}({\mathbb Z} G)$ is coherent. This reduces the problem to classify the finite groups G for which 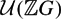$\mathcal{U}({\mathbb Z} G)$ is coherent to decide about the coherency of a finite list of groups of the form SLn(R), with R an order in a finite dimensional rational division algebra.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 162 , Issue 2 , March 2017 , pp. 191 - 209
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BS72] Benard, M. and Schacher, M. M. The Schur subgroup, II. J. Algebra 22 (1972), 378–385. MR 0302747 (46 #1890)CrossRefGoogle Scholar
[EKVG15] Eisele, F., Kiefer, A. and Van Gelder, I. Describing units of integral group rings up to commensurability. J. Pure Appl. Algebra 219 (2015), no. 7, 2901–2916. MR 3313511CrossRefGoogle Scholar
[Ger81] Gersten, S. M. Coherence in doubled groups. Comm. Algebra 9 (1981), no. 18, 1893–1900. MR 638240 (82m:20032)CrossRefGoogle Scholar
[GH87] Gow, R. and Huppert, B. Degree problems of representation theory over arbitrary fields of characteristic 0. On theorems of N. Itô and J. G. Thompson. J. Reine Angew. Math. 381 (1987), 136–147. MR 918845 (89b:20029)Google Scholar
[GH88] Gow, R. and Huppert, B. Degree problems of representation theory over arbitrary fields of characteristic 0. II. Groups which have only two reduced degrees. J. Reine Angew. Math. 389 (1988), 122–132. MR 953668 (89i:20021)Google Scholar
[Hup67] Huppert, B. Endliche Gruppen, I. Die Grundlehren der Mathematischen Wissenschaften, Band 134 (Springer-Verlag, Berlin, 1967), MR 0224703 (37 #302)CrossRefGoogle Scholar
[Isa76] Isaacs, I. M. Character Theory of Finite Groups (Academic Press [Harcourt Brace Jovanovich Publishers], New York, 1976), Pure and Applied Mathematics, No. 69. MR 0460423 (57 #417)Google Scholar
[Kle00] Kleinert, E. Two theorems on units of orders. Abh. Math. Sem. Univ. Hamburg 70 (2000), 355–358. MR 1809557CrossRefGoogle Scholar
[OdRS04] Olivieri, A., del Río, Á. and Simón, J. J. On monomial characters and central idempotents of rational group algebras. Comm. Algebra 32 (2004), no. 4, 1531–1550. MR 2100373 (2005i:16054)CrossRefGoogle Scholar
[OdRS06] Olivieri, A., del Río, Á. and Simón, J. J. The group of automorphisms of the rational group algebra of a finite metacyclic group. Comm. Algebra 34 (2006), no. 10, 3543–3567. MR 2262368 (2007g:20037)CrossRefGoogle Scholar
[Pas89] Passman, D. S. Infinite Crossed Products. Pure and Applied Mathematics, vol. 135 (Academic Press Inc., Boston, MA, 1989), MR 979094 (90g:16002)Google Scholar
[Pie82] Pierce, R. S. Associative Algebras. Graduate Texts in Mathematics, vol. 88 (Springer-Verlag, New York, 1982), Studies in the History of Modern Science, 9. MR 674652 (84c:16001)CrossRefGoogle Scholar
[Rei75] Reiner, I. Maximal Orders (Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], London-New York, 1975), London Mathematical Society Monographs, No. 5. MR 0393100 (52 #13910)Google Scholar
[Roq58] Roquette, P. Realisierung von Darstellungen endlicher nilpotenter Gruppen. Arch. Math. (Basel) 9 (1958), 241–250. MR 0097452 (20 #3921)CrossRefGoogle Scholar
[Sco73] Scott, G. P. Finitely generated 3-manifold groups are finitely presented. J. London Math. Soc. 6 (1973), 437–440. MR 0380763 (9,224e)CrossRefGoogle Scholar
[Seh93] Sehgal, S. K. Units in Integral Group Rings. Pitman Monographs and Surveys in Pure and Applied Mathematics, vol. 69 (Longman Scientific & Technical, Harlow, 1993), MR 1242557 (94m:16039)Google Scholar
[Ser79] Serre, J.-P. Arithmetic Groups. Homological group theory (Proc. Sympos., Durham, 1977), London Math. Soc. Lecture Note Ser., vol. 36 (Cambridge University Press, Cambridge-New York, 1979), pp. 105–136. MR 564421 (82b:22021)Google Scholar
[Wis11] Wise, D. T. Morse theory, random subgraphs, and incoherent groups. Bull. Lond. Math. Soc. 43 (2011), no. 5, 840–848. MR 2854555CrossRefGoogle Scholar