Bounded representations of the positive values of an indefinite quadratic form
Published online by Cambridge University Press: 24 October 2008
Extract
Let
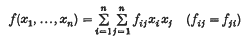
be a real quadratic form in n variables (n ≥ 2) with integral coefficients and determinant D = |fij| ≠ 0. Cassels ((1),(2)) has recently proved that if the equation f = 0 is properly soluble in integers x1, …, xn, then there is a solution satisfying
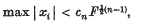
where F = max | fij and cn depends only on n. An example given by Kneser (see (2)) shows that the exponent ½(n – 1) is best possible. A simpler proof of Cassels's result has since been given by Davenport(3), and the theorem has been improved in certain cases by Watson(4). Here I consider the inequality f(x1, …, xn) > 0, where f is an indefinite form, and obtain a result analogous to that of Cassels.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 54 , Issue 1 , January 1958 , pp. 14 - 17
- Copyright
- Copyright © Cambridge Philosophical Society 1958
References
REFERENCES
- 2
- Cited by


