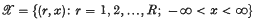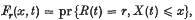Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Keilson, J.
1966.
The Ergodic Queue Length Distribution for Queueing Systems with Finite Capacity.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 28,
Issue. 1,
p.
190.
Keilson, Julian
and
Wishart, David M. G.
1967.
Addenda to processes defined on a finite Markov chain.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 1,
p.
187.
Presman, E. L.
1967.
Boundary Problems for Sums of Lattice Random Variables, Defined on a Finite Regular Markov Chain.
Theory of Probability & Its Applications,
Vol. 12,
Issue. 2,
p.
323.
Keilson, Julian
and
Rao, S. Subba
1970.
A process with chain dependent growth rate.
Journal of Applied Probability,
Vol. 7,
Issue. 3,
p.
699.
Keilson, Julian
and
Rao, S. Subba
1970.
A process with chain dependent growth rate.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
699.
Zaslavskii, A. E.
1971.
A generalization of a renewal theorem.
Siberian Mathematical Journal,
Vol. 12,
Issue. 3,
p.
362.
Brockwell, P. J.
1972.
A storage model in which the net growth-rate is a Markov chain.
Journal of Applied Probability,
Vol. 9,
Issue. 1,
p.
129.
�inlar, Erhan
1972.
Markov additive processes. I.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 24,
Issue. 2,
p.
85.
Newbould, M.
1973.
A classification of a random walk defined on a finite Markov chain.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 26,
Issue. 2,
p.
95.
Sumita, Ushio
1984.
The matrix Laguerre transform.
Applied Mathematics and Computation,
Vol. 15,
Issue. 1,
p.
1.
Keilson, Julian
1986.
The Craft of Probabilistic Modelling.
Vol. 1,
Issue. ,
p.
166.
Ramsay, Colin M.
1987.
Advances in the Statistical Sciences: Applied Probability, Stochastic Processes, and Sampling Theory.
p.
189.
Cogger, Kenneth O.
1988.
Proposals for research in time series forecasting.
International Journal of Forecasting,
Vol. 4,
Issue. 3,
p.
403.
Keilson, J.
and
Zachmann, M.
1988.
Homogeneous row-continuous bivariate markov chains with boundaries.
Journal of Applied Probability,
Vol. 25,
Issue. A,
p.
237.
Keilson, J.
and
Zachmann, M.
1988.
Homogeneous row-continuous bivariate markov chains with boundaries.
Journal of Applied Probability,
Vol. 25,
Issue. A,
p.
237.
Asmussen, Søren
1989.
Risk theory in a Markovian environment.
Scandinavian Actuarial Journal,
Vol. 1989,
Issue. 2,
p.
69.
Gerontidis, Ioannis I.
1993.
A continuous time markov‐renewal replacement model for manpower systems.
Applied Stochastic Models and Data Analysis,
Vol. 9,
Issue. 1,
p.
39.
Gerontidis, Ioannis I.
1994.
Periodic Markovian replacement chains.
Stochastic Processes and their Applications,
Vol. 51,
Issue. 2,
p.
307.
Meng, Qingbin
Li, Zhendong
and
Zhang, Peng
2008.
On the Dividend for the Markov-Switching Risk Model.
p.
1.
Sumita, Ushio
Huang, Jia-Ping
and
Dshalalow, Jewgeni
2009.
Dynamic Analysis of a Unified Multivariate Counting Process and Its Asymptotic Behavior.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2009,
Issue. 1,