Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-20T00:49:58.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Base conditions and covariant systems in an algebraic threefold

Published online by Cambridge University Press:  24 October 2008

J. G. Semple
J. G. Semple
Affiliation:
King's CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

If F is a free linear system of surfaces in an algebraic threefold V which is either non-singular or possesses only normal singularities, then F has Jacobian and adjoint surfaces, J2(F) and A2(F), and Jacobian and adjoint curve systems, J1(F) and A1(F), such that

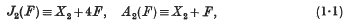
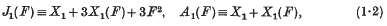
where X2, X2 are the canonical systems of surfaces and curves on V, and X1(F) is the canonical system of curves of F. The imposition of base elements (points or curves) Ei, of assigned multiplicities λi, on F defines a system F1 which we may represent formally by the equation

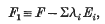
and it is natural to enquire how the Jacobian systems of F1 differ from those of F, and how we may define adjoint systems A2(F1) and A1(F1) which cut on F1 its canonical curves and sets respectively.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 2 , April 1939 , pp. 166 - 179
Copyright
Copyright © Cambridge Philosophical Society 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Todd, J. A. “The geometrical invariants of algebraic loci.” Proc. London Math. Soc. (2), 43 (1937), 127.Google Scholar
(2)Todd, J. A. “Birational transformations with isolated fundamental points.” Proc. Edinburgh Math. Soc. (2), 5 (1937), 117.CrossRefGoogle Scholar
(3)Todd, J. A. “Birational transformations possessing fundamental curves.” Proc. Cambridge Phil. Soc. 34 (1938), 144.CrossRefGoogle Scholar
(4)Segre, B. “Nuovi contributi alla geometria sulle varietà algebriche.” Mem. R. Accad. Ital. 5 (1934), 479.Google Scholar
(5)Eger, M. “Sur les systèmes canoniques d'une variété algébrique.” Comptes rendus, 204 (1937), 217.Google Scholar
(6)Enriques, F.Teoria delle superficie algebriche (Padova, 1932).Google Scholar
(7)Baker, H. F.Principles of geometry, vol. 6 (Cambridge, 1933).Google Scholar
(8)Babbage, D. W. “Isolated singular points in the theory of algebraic surfaces.” Proc. Cambridge Phil. Soc. 29 (1933), 212.CrossRefGoogle Scholar
(9)Noether, M. “Sulle curve multiple di superficie algebriche.” Annali di Mat. (2), 5 (1871), 164.Google Scholar