Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T08:34:24.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Attaching cells to finite complexes, with an application to elliptic spaces

Published online by Cambridge University Press:  24 October 2008

Geoffrey M. L. Powell
Geoffrey M. L. Powell
Affiliation:
The Mathematical Institute, 24–29 St Giles', Oxford, OX1 3LB
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that f; Sn → E is a continuous map from the n-sphere to a 1-connected CW complex E, with n ≥ 2. One may suppose that f is a cofibration, so that there is a cofibration sequence 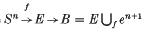, with f the attaching map of the cell en+1. Consider the homotopy fibre F of the inclusion E ↪ B, so that there is a homotopy fibration 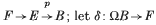let δ; ΩB → F be the connectant of this fibration. The following definition is given by Félix and Lemaire in [11]: Definition 1·1. Suppose that k is a field of characteristic p ≥ 0. The attaching map f:Sn → E is: 1. p-inert if 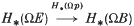is surjective; 2. p-lazy if 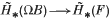is zero; where H˜ denotes reduced homology and coefficients are taken in the field k.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 3 , April 1996 , pp. 483 - 491
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F. and Hilton, P. J.. On the chain algebra of a loop space. Comment. Math. Helv. 30 (1955), 305–330.CrossRefGoogle Scholar
[2]Anick, D. J.. Non-commutative graded algebras and their Hubert series. J. Algebra 78 (1982), 120–140.CrossRefGoogle Scholar
[3]Anick, D. J.. Hopf algebras up to homotopy. J. Amer. Math. Soc. 2, no. 3 (1989), 417–453.CrossRefGoogle Scholar
[4]Anick, D. J.. Homotopy exponents for spaces of category two, in Algebraic Topology: Proceedings, Arcata, 1986. Lecture Notes in Math. 1370 (Springer-Verlag), pp. 24–52.Google Scholar
[5]Cohen, F., Moore, J. C. and Neisendorfer, J. A.. Torsion in homotopy groups. Ann. of Math. (2) 109 (1979), 121–168.CrossRefGoogle Scholar
[6]Felix, Y.. La dichotomie elliptique-hyperbolique en homotopie rationnelle. S.M.F. Astérisque 176 (1989).Google Scholar
[7]Felix, Y., Halperin, S. and Thomas, J.-C.. Elliptic Hopf algebras. J. London Math. Soc. (2) 43 (1991), 545–555.CrossRefGoogle Scholar
[8]Felix, Y., Halperin, S. and Thomas, J.-C.. Gorenstein spaces. Adv. in Math. 71 (1988), 92–112.CrossRefGoogle Scholar
[9]Felix, Y., Halperin, S. and Thomas, J.-C.. Elliptic spaces. Bull. Amer. Math. Soc. 25 (1991), 69–73.CrossRefGoogle Scholar
[10]Felix, Y., Halperin, S. and Thomas, J.-C.. Elliptic spaces II. Enseign. Math. (2) 39 (1993), 25–32.Google Scholar
[11]Felix, Y. and Lemaire, J.-M.. On the Pontrjagin algebra of the loops on a space with a cell attached. Internat. J. Math. 2 (1991), 429–438.CrossRefGoogle Scholar
[12]Felix, Y. and Thomas, J.-C.. Module d'holonomie d'une fibration. Bull. Soc.Math. France 113 (1985), 255–258.CrossRefGoogle Scholar
[13]Halperin, S.. Universal enveloping algebras and loop space homology. J. Pure and Applied Algebra 83 (1992), 237–282.CrossRefGoogle Scholar
[14]Lemaire, J.-M.. Algebres connexes et homologie des espaces de lacets, Lecture Notes in Math. Vol. 422 (Springer-Verlag, 1974).CrossRefGoogle Scholar
[15]Lemaire, J.-M.. Autopsie d'un meurtre dans l'homologie d'une algèbre de chaines. Ann. Sci. Ecole Norm. Sup. 11 (1978), 93–100.CrossRefGoogle Scholar
[16]Mccleary, J.. On the mod p Betti numbers of loop spaces. Invent. Math. 87 (1987), 643–654.CrossRefGoogle Scholar
[17]Powell, G. M. L.. D.Phil Thesis (Oxford, 1994).Google Scholar
[18]Tanre, D.. Homotopie rationelle: modèles de Chen, Quillen, Sullivan, Lecture Notes in Math. Vol. 1025 (Springer-Verlag, 1983).CrossRefGoogle Scholar