Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T21:11:17.398Z Has data issue: false hasContentIssue false
  • English
  • Français

The associated graded ring of an integral group ring

Published online by Cambridge University Press:  24 October 2008

Inder Bir S. Passi  and
Lekh Raj Vermani
Inder Bir S. Passi
Affiliation:
B. N. Chakravarty University, Kurukshetra, India
Lekh Raj Vermani
Affiliation:
B. N. Chakravarty University, Kurukshetra, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be an Abelian group, 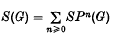the symmetric algebra of G and 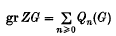the associated graded ring of the integral group ring ZG, where 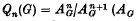(AG denotes the augmentation ideal of ZG). Then there is a natural epimorphism (4)

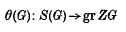
which is given on the nth component by

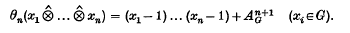
In general θ is not an isomorphism. In fact Bachmann and Grünenfelder(1) have shown that for finite Abelian G, θ is an isomorphism if and only if G is cyclic. Thus it is of interest to investigate ker θn for finite Abelian groups. In view of proposition 3.25 of (3) it is enough to consider finite Abelian p-groups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 1 , July 1977 , pp. 25 - 33
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bachmann, F. and GrüNenfelder, L.Über Lie-Ringe von Gruppen und ihre universellen Enveloppen. Comment. Math. Helv. 47 (1972), 332–340.CrossRefGoogle Scholar
(2)Bachmann, F. and Grünenfelder, L.The periodicity in the graded ring associated with an integral group ring. J. Pure and Applied Algebra 5 (1974), 253–264.CrossRefGoogle Scholar
(3)Passi, I. B. S.Polynomial maps on groups. J. Algebra 9 (1968), 121–151.CrossRefGoogle Scholar
(4)Passi, I. B. S.Polynomial functors. Proc. Cambridge Philos. Soc. 66 (1969), 505–512.CrossRefGoogle Scholar
(5)Sandling, R.Modular augmentation ideals. Proc. Cambridge Philos. Soc. 71 (1972), 25–32.CrossRefGoogle Scholar
(6)Serre, J. P. Algèbre locale. Multiplicités. Lecture Notes in Mathematics 11 (Berlin, Heidelberg, New York, Springer 1965).Google Scholar
(7)Singer, M.On the graded ring associated with an integral group ring. Communications in Algebra 3 (11) (1975), 1037–1049.CrossRefGoogle Scholar
(8)Vermani, L. R.On polynomial groups. Proc. Cambridge Philos. Soc. 68 (1970), 285–289.CrossRefGoogle Scholar
(9)Wilson, J. C. R. Polynomial functors on Abelian groups. (To appear.)Google Scholar