Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T21:16:14.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic continuation of multiple Hurwitz zeta functions

Published online by Cambridge University Press:  01 November 2008

JAMES P. KELLIHER  and
RIAD MASRI
JAMES P. KELLIHER
Affiliation:
Brown University, Department of Mathematics, 151 Thayer Street, Providence, RI 02912, U.S.A. e-mail: [email protected]
RIAD MASRI
Affiliation:
I. H. É. S., Le Bois-Marie, 35, Route De Chartres F-91440, Bures-Sur-Yvette, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

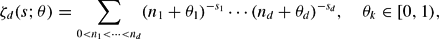
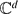We use a variant of a method of Goncharov, Kontsevich and Zhao [5, 16] to meromorphically continue the multiple Hurwitz zeta functionto , to locate the hyperplanes containing its possible poles and to compute the residues at the poles. We explain how to use the residues to locate trivial zeros of .

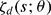Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 3 , November 2008 , pp. 605 - 617
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akiyama, S. and Ishikawa, H.On analytic continuation of multiple L-functions and related zeta-functions. Analytic number theory (Beijing/Kyoto, 1999) Dev. Math. 6 (2002), 1–16.CrossRefGoogle Scholar
[2]Beĭlinson, A. and Deligne, P.Interprétation motivique de la conjecture de Zagier reliant polylogarithmes et régulateurs, Motives (Seattle, WA, 1991). Proc. Sympos. Pure Math. 55, Part 2 (1994), 97–121.CrossRefGoogle Scholar
[3]Borwein, J. M., Bradley, D. M., Broadhurst, D. J. and Lisonek, P.Combinatorial aspects of multiple zeta values. Electron. J. Combin. 5 (1998), Research Paper 38, 12 pp.CrossRefGoogle Scholar
[4]Goncharov, A. B.Volumes of hyperbolic manifolds and mixed Tate motives. J. Amer. Math. Soc. 12 (1999), 569–618.CrossRefGoogle Scholar
[5]Goncharov, A. B. Multiple polylogarithms and mixed Tate motives, at math archives.Google Scholar
[6]Gunning, R. C.Introduction to Holomorphic Functions of Several Complex Variables, Volume I, Function Theory (Wadsworth, Inc., 1990).Google Scholar
[7]Gunning, R. C.Introduction to Holomorphic Functions of Several Complex Variables, Volume II, Local Theory (Wadsworth, Inc., 1990).Google Scholar
[8]Kontsevich, M.Vassiliev's Knot Invariants, I. M. Gel'fand Seminar. Adv. Soviet Math. 16, Part 2 (1993), 137–150.Google Scholar
[9]Kontsevich, M.Operads and motives in deformation quantization. Lett. Math. Phys. 48 (1999), 35–72.CrossRefGoogle Scholar
[10]Ram Murty, M. and Sinha, K.Multiple Hurwitz zeta functions. Multiple Dirichlet series, automorphic forms, and analytic number theory, 135–156, Proc. Sympos. Pure Math. 75, Amer. Math. Soc., Providence, RI (2006).Google Scholar
[11]Minh, H., Jacob, G., Gérard, P., Petitot, M. and Oussous, N.De l'algèbre des ζ de Riemann multivariées à l'algèbre des ζ de Hurwitz multivariées. Sém. Lothar. Combin. 44 (2000), Art. B44i, 21 pp.Google Scholar
[12]Stein, E. M.Singular Integrals and Differentiability Properties of Functions (Princeton University Press, 1970).Google Scholar
[13]Terasoma, T.Mixed Tate motives and multiple zeta values. Invent. Math. 149 (2002), 339–369.CrossRefGoogle Scholar
[14]Zagier, D.Values of zeta functions and their applications. First European Congress of Mathematics, Vol. II (Paris, 1992) Progr. Math. 120 (1994), 497–572.Google Scholar
[15]Zagier, D. Periods of modular forms, traces of Hecke operators, and multiple zeta values. Sūrikaisekikenkyūsho Kōkyūroku, (843) (1993), 162–170. Research into automorphic forms and L-functions (Japanese) (Kyoto, 1992).Google Scholar
[16]Zhao, J.Analytic continuation of multiple zeta functions. Proc. Amer. Math. Soc. 128 (1999), 1275–1283.CrossRefGoogle Scholar