Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ruzsa, Imre
and
Solymosi, Jozsef
2022.
Sumsets of semiconvex sets.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 1,
p.
84.
Bradshaw, Peter J.
2023.
Growth in Sumsets of Higher Convex Functions.
Combinatorica,
Vol. 43,
Issue. 4,
p.
769.
Dona, Daniele
2023.
A sum-bracket theorem for simple Lie algebras.
Journal of Algebra,
Vol. 631,
Issue. ,
p.
658.
Mansfield, Sam
and
Mudgal, Akshat
2024.
A quadratic Vinogradov mean value theorem in finite fields.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
1007.
ROCHE–NEWTON, OLIVER
2024.
A better than
$3/2$
exponent for iterated sums and products over
$\mathbb R$
.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 177,
Issue. 1,
p.
11.
Dettmann, Carl P.
and
Taylor-West, Liam
2024.
Algebraic tunings.
Journal of Mathematics and Music,
Vol. 18,
Issue. 2,
p.
203.
Orponen, Tuomas
2024.
On the discretised 𝐴𝐵𝐶 sum-product problem.
Transactions of the American Mathematical Society,
Jing, Yifan
and
Mudgal, Akshat
2025.
Finding large additive and multiplicative Sidon sets in sets of integers.
Mathematische Annalen,
Vol. 391,
Issue. 1,
p.
685.
Clevenger, Ginny Ray
Havard, Haley
Heard, Patch
Lott, Andrew
Rice, Alex
and
Wilson, Brittany
2025.
The sum-product problem for small sets.
Involve, a Journal of Mathematics,
Vol. 18,
Issue. 1,
p.
165.
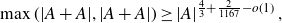 \[\max(|A+A|,|A+A|)\geq |A|^{\frac{4}{3} + \frac{2}{1167} - o(1)}\,,\]
\[\max(|A+A|,|A+A|)\geq |A|^{\frac{4}{3} + \frac{2}{1167} - o(1)}\,,\]
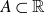 $A\subset \mathbb {R}$
, following a streamlining of the arguments of Solymosi, Konyagin and Shkredov. We include several new observations to our techniques.
$A\subset \mathbb {R}$
, following a streamlining of the arguments of Solymosi, Konyagin and Shkredov. We include several new observations to our techniques.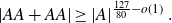 \[|AA+AA|\geq |A|^{\frac{127}{80} - o(1)}\,.\]
This paper is largely self-contained.
\[|AA+AA|\geq |A|^{\frac{127}{80} - o(1)}\,.\]
This paper is largely self-contained.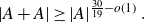 \[|A+A|\geq |A|^{\frac{30}{19}-o(1)}\,.\]
\[|A+A|\geq |A|^{\frac{30}{19}-o(1)}\,.\]