No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
It has been shown by Kulakoff that if G is a group, not cyclic, of order pl, p being an odd prime, the number of subgroups of G of order pk, for 0 < k < l, is congruent to 1 + p (mod p2); and by Hall that if G is any group of finite order whose Sylow subgroups of G of order pk, p being odd, are not cyclic, then, for 0 < k < l, the number of subgroups of G of order pk is congruent to 1 + p (mod p2). No results were given for the case p = 2. In the present paper it is shown that analogous results hold for the case p = 2, but that the role of the cyclic groups is played by groups of four exceptional types: the cyclic groups themselves, and three non-Abelian types. These groups are defined as follows:
(1) The dihedral group, of order 2k, generated by A and B, where
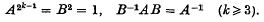
(2) The quaternion group, of order 2k, generated by A and B, where
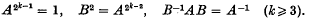
(3) The "mixed" group, of order 2k, generated by A and B, where
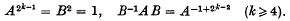
† Math. Ann. 101 (1931), 779.Google Scholar
‡ Proc. London Math. Soc. (2), 40 (1935), 500.Google Scholar
† See Bumside, , Theory of groups, 2nd ed. (Cambridge, 1911), p. 146;Google Scholar types ii, vi.
‡ Hall, , Proc. London Math. Soc. (2), 36 (1932), 39.Google Scholar