Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T13:53:09.893Z Has data issue: false hasContentIssue false
  • English
  • Français

An asymptotic bound for the residual area of a packing of discs

Published online by Cambridge University Press:  24 October 2008

D. G. Larman
D. G. Larman
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that a sequence of discs

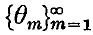
arranged in decreasing order of diameters, forms a packing within the unit plane square I2. It has been shown, by Florian(1), that the area of

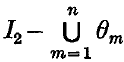
is at least O(a), where a is the radius of θn. However, Gilbert (2) has produced some empirical results for the Apollonius packing 71 of discs which seem to suggest that for such a packing, the area of the set

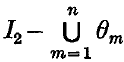
is at least O(as) for some positive real number s, less than one. As Gilbert remarks, it is difficult to imagine that the Apollonius packing is not the extremal case, and so, that it would seem likely that there exists a positive real number s, less than one, such that for a general packing, the area of

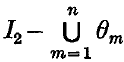
is at least O(as). The purpose of this paper is to establish this result by showing that 0·97 is an allowable value for s.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 4 , October 1966 , pp. 699 - 704
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Florian, A.Ausfullung der Ebene durch Kreise. Rend. Circ. Mat. Palermo, II, 9 (1960), 300–312.CrossRefGoogle Scholar
(2)Gilbert, E. N.Randomly packed and solidly packed spheres. Can. J. Math. 16 (1964), 286–298.Google Scholar
(3)Larman, D. G.On the Besicovitch dimension of the residual set of arbitrarily packed discs in the plane. Accepted for publication in J. London Math. Soc.Google Scholar