An approximate treatment of high-frequency scattering
Published online by Cambridge University Press: 24 October 2008
Extract
In some recent work Kodis* considers the scattering of a plane harmonic wave by a circular cylinder and uses variational methods to deduce an asymptotic formula for the scattering coefficient in the case of high-frequency waves. The scattering coefficient, σ, is denned as the total energy flux outward from the cylinder in the scattered wave divided by the energy flux in the beam of the incident wave which falls on the cylinder. In the limit, of geometrical optics, the scattered wave is made up of a wave reflected from the forward half of the cylinder with energy flux equal to that in the incident beam, and a wave behind the cylinder cancelling the incident wave there to form the shadow. Thus σ → 2 as ka → ∞, k being the wave number of the incident wave and a the radius of the cylinder. The next term in the asymptotic expansion for σ is proportional to 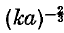 . It has been determined already from the exact series expression for the field by White (6), Wu and Rubinow (7) and Kear (3). But Kodis gives an approximate method which also supplies this result and, since the coefficient is in good agreement with the values obtained from the exact solution, concludes that his approximate procedure could also be used for more general obstacles. In the present paper, we propose an alternative approximate method which is related to the one given by Kodis but is very much simpler. Also we go on to obtain the correction terms for general obstacles in detail. Various writers (see, for example, Keller (4) and van de Hulst(8)) have suggested previously that the correction is still proportional to
. It has been determined already from the exact series expression for the field by White (6), Wu and Rubinow (7) and Kear (3). But Kodis gives an approximate method which also supplies this result and, since the coefficient is in good agreement with the values obtained from the exact solution, concludes that his approximate procedure could also be used for more general obstacles. In the present paper, we propose an alternative approximate method which is related to the one given by Kodis but is very much simpler. Also we go on to obtain the correction terms for general obstacles in detail. Various writers (see, for example, Keller (4) and van de Hulst(8)) have suggested previously that the correction is still proportional to 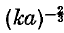 , where a is some length defined by the body shape. However, the determination of a and of the numerical coefficient has been limited to two-dimensional obstacles.
, where a is some length defined by the body shape. However, the determination of a and of the numerical coefficient has been limited to two-dimensional obstacles.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 3 , July 1957 , pp. 691 - 701
- Copyright
- Copyright © Cambridge Philosophical Society 1957
References
REFERENCES
- 6
- Cited by


