An application of descent to a classification theorem for toposes
Published online by Cambridge University Press: 24 October 2008
Extract
The aim of this paper is to answer the following question. For a spatial groupoid G, i.e. for a groupoid in the category Sp of spaces (in the sense of [20]) in a topos 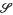 , and continuous maps, the topos BG, of étale G-spaces, is called ‘the classifying topos of G’ by Moerdijk[22]. This terminology is suggested by the case of G a discrete group (in Sets), as then BG, the topos of G-sets, classifies principal G-bundles. This means that, for each topological space X, there is a bijection between isomorphism classes of principal G-bundles over X and isomorphism classes of geometric morphisms from Sh(X) to BG. The question is: what does BG classify, in terms of G, in the general case of a spatial groupoid G in a topos
, and continuous maps, the topos BG, of étale G-spaces, is called ‘the classifying topos of G’ by Moerdijk[22]. This terminology is suggested by the case of G a discrete group (in Sets), as then BG, the topos of G-sets, classifies principal G-bundles. This means that, for each topological space X, there is a bijection between isomorphism classes of principal G-bundles over X and isomorphism classes of geometric morphisms from Sh(X) to BG. The question is: what does BG classify, in terms of G, in the general case of a spatial groupoid G in a topos 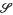 ?
?
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 107 , Issue 1 , January 1990 , pp. 59 - 79
- Copyright
- Copyright © Cambridge Philosophical Society 1990
References
REFERENCES
- 13
- Cited by


