Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T14:38:20.400Z Has data issue: false hasContentIssue false
  • English
  • Français

a-convexity

Published online by Cambridge University Press:  24 October 2008

R. G. E. Pinch
R. G. E. Pinch
Affiliation:
Department of Mathematics, University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Extract

For a ε R, we define a subset V of Rn to be a-convex if x, y ε V implies

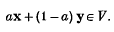
Clearly V is (1 — a)-convex iff it is a-convex: V is convex iff it is a-convex for all a ε [0, 1], and any set is 1-convex. We define the a-convex hull of V to be the intersection of all a-convex subsets of Rn containing V. Put D = 0,1} and D(a) the a-convex hull of D in R1. If V is a-convex and x, y ε V, then V must contain the points of the line through x, y given by {tx + (1 — t) y: t ε D(a)} and so in this paper we concentrate on the study of D(a).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 1 , January 1985 , pp. 63 - 68
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Calvert, I.. On the closure of a class of subsets of the real line. Math. Proc. Cambridge Philos. Soc. 83 (1978), 181–182.CrossRefGoogle Scholar
[2]Samuel, P.. Algebraic Theory of Numbers (Hermann/Kershaw, 1972).Google Scholar