3-transpositions in infinite groups
Published online by Cambridge University Press: 24 October 2008
Extract
Let G be a group. A subset D will be called a set of 3-transpositions if |x| = 2 for xεD and |xy| = 3 whenever x, yεD do not commute. We will call the set D closed if xDx−1 = D for each xεD. For each xεD, let
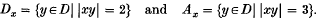
For each subset X of D, we denote by [X] the graph with vertex set X where two elements x, yεX are joined by an edge whenever they commute. We denote by (X) the complement graph; thus two elements x, yεX are joined by an edge of (X) whenever they do not commute.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 3 , November 1984 , pp. 371 - 377
- Copyright
- Copyright © Cambridge Philosophical Society 1984
References
REFERENCES
[1]Aschbacher, M.. A homomorphism theorem for finite graphs. Proc. Amer. Math. Soc. 54 (1976), 468–470.CrossRefGoogle Scholar
[2]Blass, A.. Graphs with unique maximal dumpings. J. Graph Theory 2 (1978), 19–24.CrossRefGoogle Scholar
[3]Fischer, B.. Finite groups generated by 3-transpositions. Invent. Math. 13 (1971), 232–246 and University of Warwick Lecture Notes (unpublished).Google Scholar
- 6
- Cited by


