Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-07T12:33:48.913Z Has data issue: false hasContentIssue false
  • English
  • Français

The abelianization of the congruence IA-automorphism group of a free group

Published online by Cambridge University Press:  10 April 2007

TAKAO SATOH
TAKAO SATOH*
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, Komaba, Tokyo, 153-8914, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the abelianizations of some normal subgroups of the automorphism group of a finitely generated free group. Let Fn be a free group of rank n. For d ≥ 2, we consider a group consisting the automorphisms of Fn which act trivially on the first homology group of Fn with 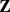/d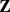-coefficients. We call it the congruence IA-automorphism group of level d and denote it by IAn,d. Let IOn,d be the quotient group of the congruence IA-automorphism group of level d by the inner automorphism group of a free group. We determine the abelianization of IAn,d and IOn,d for n ≥ 2 and d ≥ 2. Furthermore, for n=2 and odd prime p, we compute the integral homology groups of IA2,p for any dimension.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 142 , Issue 2 , March 2007 , pp. 239 - 248
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Arlettaz, D.. On the homology and cohomology of congruence subgroups. J. Pure Appl. Alg. 44 (1987), 3–12.CrossRefGoogle Scholar
[2] Cohen, F. and Pakianathan, J.. On automorphism groups of free groups, and their nilpotent quotients. Preprint.Google Scholar
[3] Cohen, F. and Pakianathan, J.. On subgroups of the automorphism group of a free group and associated graded lie algebras. Preprint.Google Scholar
[4] Farb, B.. Automorphisms of Fn which act trivially on homology. In preparation.Google Scholar
[5] Frasch, H.. Die erzeugenden der hauptkongruenzgruppen für primzahlstufen. Math. Ann. 108 (1933), 230–252.CrossRefGoogle Scholar
[6] Gersten, S. M.. A presentation for the special automorphism group of a free group. J. Pure Appl. Alg. 33 (1984), 269–279.Google Scholar
[7] Hatcher, A. and Vogtmann, K.. Rational homology of Aut(Fn). Math. Res. Lett. 5 (1998), 759–780.CrossRefGoogle Scholar
[8] Kawazumi, N.. Cohomological aspects of Magnus expansions. Preprint, The University of Tokyo. UTMS 2005-18 (2005), http://www.yukawa.kyoto-u.ac.jp/abs/math.GT/0505497.Google Scholar
[9] Krstić, S. and McCool, J.. The non-finite presentability in IA(F3) and GL2(Z]t, t−1]). Invent. Math. 129 (1997), 595–606.Google Scholar
[10] Lee, R. and Szczarba, R. H.. On the homology and cohomology of congruence subgroups. Invent. Math. 33 (1976), 15–53.Google Scholar
[11] Magnus, W.. Über n-dimensinale Gittertransformationen. Acta Math. 64 (1935), 353–367.Google Scholar
[12] Nielsen, J.. Die Isomorphismen der allgemeinen unendlichen gruppe mit zwei erzeugenden. Math. Ann. 78 (1918), 385–397.CrossRefGoogle Scholar
[13] Nielsen, J.. Die isomorphismengruppe der freien gruppen. Math Ann. 91 (1924), 169–209.Google Scholar
[14] Reutenauer, C.. Free lie algebras. London Math. Soc. Monogr. (N.S.) no. 7 (1993).Google Scholar