Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T14:03:39.775Z Has data issue: false hasContentIssue false
  • English
  • Français

3-transpositions in infinite groups

Published online by Cambridge University Press:  24 October 2008

Richard Weiss
Richard Weiss
Affiliation:
Department of Mathematics, Tufts University, Medford, MA 02155, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a group. A subset D will be called a set of 3-transpositions if |x| = 2 for xεD and |xy| = 3 whenever x, yεD do not commute. We will call the set D closed if xDx−1 = D for each xεD. For each xεD, let

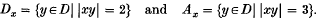
For each subset X of D, we denote by [X] the graph with vertex set X where two elements x, yεX are joined by an edge whenever they commute. We denote by (X) the complement graph; thus two elements x, yεX are joined by an edge of (X) whenever they do not commute.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 3 , November 1984 , pp. 371 - 377
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aschbacher, M.. A homomorphism theorem for finite graphs. Proc. Amer. Math. Soc. 54 (1976), 468–470.CrossRefGoogle Scholar
[2]Blass, A.. Graphs with unique maximal dumpings. J. Graph Theory 2 (1978), 19–24.CrossRefGoogle Scholar
[3]Fischer, B.. Finite groups generated by 3-transpositions. Invent. Math. 13 (1971), 232–246 and University of Warwick Lecture Notes (unpublished).Google Scholar