Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T06:03:30.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat Transfer in a Medium in Which Many Small Particles AreEmbedded

Published online by Cambridge University Press:  28 January 2013

A. G. Ramm
Get access

Abstract

The heat equation is considered in the complex system consisting of many small bodies(particles) embedded in a given material. On the surfaces of the small bodies aNewton-type boundary condition is imposed. An equation for the limiting field is derivedwhen the characteristic size a of the small bodies tends to zero, theirtotal number \hbox{$\mathcal{N}(a)$}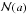𝒩(a) tends to infinity at a suitable rate, and the distanced = d(a) between neighboring smallbodies tends to zero a <  < d. No periodicity isassumed about the distribution of the small bodies.

Keywords

heat transfermany-body problem
Type
Research Article
Information
Mathematical Modelling of Natural Phenomena , Volume 8 , Issue 1: Harmonic analysis , 2013 , pp. 193 - 199
Copyright
© EDP Sciences, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

V. Jikov, S. Kozlov, O. Oleinik. Homogenization of differential operators and integral functionals. Springer, Berlin, 1994.
V. Marchenko, E. Khruslov. Homogenization of partial differential equations. Birkhäuser, Boston, 2006.
D. Gioranescu, P. Donato. An introduction to homogenization. Oxford Univ. Press, Oxford, 1999.
A. Bensoussan, J.-L.Lions, G. Papanicolau. Asymptotic analysis for periodic structures. AMS Chelsea Publishing, Providence, RI, 2011.
A. G. Ramm. Wave scattering by small bodies of arbitrary shapes. World Sci. Publishers, Singapore, 2005.
A.G. Ramm. Inverse problems. Springer, New York, 2005.
Ramm, A.G.. Wave scattering by many small bodies and creating materials with a desired refraction coefficient. Afrika Matematika, 22, No. 1, (2011), 33–55. CrossRefGoogle Scholar
Ramm, A.G.. A collocation method for solving integral equations. Internat. Journ. Comp. Sci and Math., 3, No. 2, (2009), 222–228. CrossRefGoogle Scholar
Ramm, A.G.. Inversion of the Laplace transform from the real axis. Inverse problems, 2, (1986), L55–59. CrossRefGoogle Scholar
A.G. Ramm, S. Indratno. Inversion of the Laplace transform from the real axis using an adaptive iterative method. Internat. Jour. Math. Math. Sci (IJMMS). Vol. 2009, Article 898195, 38 pages.
Ramm, A.G.. Sufficient conditions for zero not to be an eigenvalue of the Schrödinger operator. J. Math. Phys., 28, (1987), 1341–1343. CrossRefGoogle Scholar
Ramm, A.G.. Conditions for zero not to be an eigenvalue of the Schrödinger operator. J. Math. Phys. 29, (1988), 1431–1432. CrossRefGoogle Scholar
Ramm, A.G.. Many-body wave scattering by small bodies and applications. J. Math. Phys., 48, No. 10, (2007), 103511. CrossRefGoogle Scholar
Ramm, A.G.. Wave scattering by many small particles embedded in a medium. Phys. Lett. A, 372/17, (2008), 3064–3070. CrossRefGoogle Scholar
Ramm, A.G.. A method for creating materials with a desired refraction coefficient. Internat. Journ. Mod. Phys B, 24, No. 27, (2010), 5261–5268. CrossRefGoogle Scholar
Ramm, A.G.. Materials with a desired refraction coefficient can be created by embedding small particles into a given material. International Journal of Structural Changes in Solids (IJSCS), 2, No. 2, (2010), 17–23. Google Scholar
Ramm, A.G.. Distribution of particles which produces a ”smart” material. Jour. Stat. Phys., 127, No. 5, (2007), 915–934. CrossRefGoogle Scholar
Ramm, A.G.. Scattering of scalar waves by many small particles. AIP Advances, 1, (2011), 022135. CrossRefGoogle Scholar
Ramm, A.G.. Scattering of electromagnetic waves by many small cylinders. Results in Physics, 1, No. 1, (2011), 13–16. CrossRefGoogle Scholar