We give a survey of results on global stability for deterministic compartmental epidemiologicalmodels. Using Lyapunov techniques we revisit a classical result, and give a simple proof.By the same methods we also give a new result on differential susceptibility and infectivity modelswith mass action and an arbitrary number of compartments. These models encompass the so-calleddifferential infectivity and staged progression models. 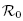In the two cases we prove that if the basicreproduction ratio $\mathcal{R}_0$ ≤ 1, then the disease free equilibrium is globally asymptotically stable. If $\mathcal{R}_0$ 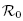> 1, there exists an unique endemic equilibrium which is asymptotically stable on the positive orthant.