In her paper (Gazette, May 1950, p. 94) on the roots of two types of determinantal equation, M. J. Moore obtained various results by elementary but somewhat complicated methods . In this note, these results are obtained by a simpler method, which moreover helps to exhibit their real significance. The essential facts are expressed by the following theorem:
THEOREM I. If a rational function of x has poles and zeros (including a possible pole or zero at infinity) which are all real, simple and strictly alternate, then its partial fraction expansion
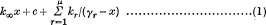
has coefficients kr (including k∞ if non-zero) all of one sign, while its reciprocal has expansion coefficients all of the opposite sign.