Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T08:56:51.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Writing a rational number in Egyptian form

Published online by Cambridge University Press:  01 August 2016

Astrid Bönning ,
Peter Hilton  and
Jean Pedersen
Astrid Bönning
Affiliation:
Sigmund-Schuckert-Gymnasium, Nürnberg 90451, Nürnberg, Germany email: [email protected]
Peter Hilton
Affiliation:
Department of Mathematical Sciences, SUNY Binghamton, Binghamton, New York 13902-6000, USA email: [email protected]
Jean Pedersen
Affiliation:
Department of Mathematics and Computer Science, Santa Clara University, Santa Clara, California 95053-0290, USA email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

A rational number 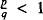is said to be expressed in Egyptian form (or Egyptian presentation) if it is written as a sum of fractions where each fraction has the numerator 1 and all of the denominators are distinct. The individual terms of die sum are often referred to as unit fractions. The problem of finding such expressions, and many related questions, has a long history, apparently beginning with Ahmes in the Rhind Papyrus. It is for this reason that we talk of ‘Egyptian’ form.

Type
Articles
Information
The Mathematical Gazette , Volume 86 , Issue 507 , November 2002 , pp. 432 - 436
Copyright
Copyright © The Mathematical Association 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Stewart, B. M., Sums of distinct divisors, Amer. J. Math. 76 (1954), pp. 779–785.Google Scholar
2. http://www-history.mcs.st-and.ac.uk/~history Google Scholar
3. Beck, Anatole, Bleicher, Michael N. and Crowe, Donald W., Excursions into mathematics, (5th printing), Worth Publishers, Inc., (1982).Google Scholar
4. Eves, Howard, An introduction to the history of mathematics, with cultural connections (by Eves, Jamie H.), (6th edn), The Saunders Series, (1992).Google Scholar
5. Bleicher, M. N., A new algorithm for the expansion of Egyptian fractions, Journal of Number Theory 4 (1972) pp. 342–382.Google Scholar
6. Erdós, P. and Stein, S., Sums of distinct unit fractions, Proc. Amer. Math. Soc. 14 (1963) pp. 126–131.Google Scholar
7. Erdôs, and Straus, E. G., On the irrationality of certain Ahmes series, J. Indian Math. Soc. 27 (1963) pp. 129–133.Google Scholar
8. Rav, R., On the representation of a rational number as a sum of a fixed number of unit fractions, J. Reine j. Angew. Math. 222 (1966), pp. 207–213.Google Scholar
9. Brenton, Lawrence and Vasiliu, Ana, Znam’s Problem, Mathematics Magazine (to appear).Google Scholar