Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T00:25:24.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Which is bigger? An intriguing ‘double alternation’

Published online by Cambridge University Press:  23 January 2015

Takeshi Hokuto  and
Mitsuhiro Kumano
Takeshi Hokuto
Affiliation:
1-1-31, Nagi, Iseda-cho, Uji, Kyoto, 611-0044, Japane-mail:[email protected]
Mitsuhiro Kumano
Affiliation:
27-22, Ikura-honmachi, Shimonoseki, Yamaguchi, 751-0863, Japane-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The following three inequalities hold:

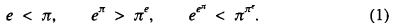
The first inequality is trivial. The second one was proved without calculating aids in note [1], and the third along similar lines in note [2]. The author of note [2] also suggested an extension to the relation between

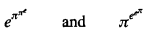
How best to continue the sequence of inequalities is not obvious and we return to that point shortly. Before doing so, we note that an interesting geralisation is to replace π by a variable x, and to determine the precise interval of x in which the regularity of the ‘alternation of inequality signs’ is maintained. We need no longer consider particular properties of π.

Type
Articles
Information
The Mathematical Gazette , Volume 98 , Issue 541 , March 2014 , pp. 67 - 72
Copyright
Copyright © The Mathematical Association 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Hill, I. D., Which is bigger – eπ or πe?, Math. Gaz. 76 (June 1986) pp.137–138.Google Scholar
2. Pinter, K., Which is bigger: ee π or ππ e?, Math. Gaz. 89 (November 2005) pp.470–471.Google Scholar