Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T14:35:52.136Z Has data issue: false hasContentIssue false
  • English
  • Français

Variations on a theme – Euler and the logsine integral

Published online by Cambridge University Press:  23 January 2015

Nick Lord
Nick Lord*
Affiliation:
Tonbridge School, Kent TN9 1JP
Get access Rights & Permissions [Opens in a new window]

Extract

This article concerns the evaluation of the ‘logsine’ integral

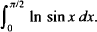
We shall encounter it in several guises. Indeed, standard integration techniques used below readily show that (1) has the same value as the following integrals:

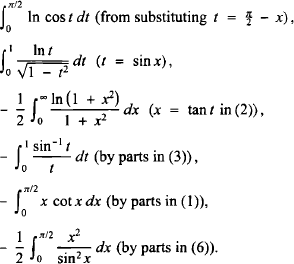
En passant, it is worth noting that forms (6) and (7) are the best behaved for numerical integration.

I first met the logsine integral as a callow youth in that strange hinterland of results that you may not have met at school but were not guaranteed to meet later on either.

Type
Articles
Information
The Mathematical Gazette , Volume 96 , Issue 537 , November 2012 , pp. 451 - 458
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ferrar, W. L., Integral calculus, Oxford University Press (1958) pp.120–121.Google Scholar
2. Siddons, A. W., Snell, K. S. and Morgan, J. B., A new calculus: Part III, Cambridge University Press (1965) pp. 103–104.Google Scholar
3. Tranter, C. J., Techniques of mathematical analysis, English Universities Press (1957) pp. 288–289.Google Scholar
4. Arora, A. K., Goel, S. K. and Rodriguez, D. M., Special integration techniques for trigonometric integrals, Amer. Math. Monthly 95 (1988) pp. 126–130.Google Scholar
5. Boros, G. and Moll, V. H., Irresistible integrals, Cambridge University Press (2004) Chapter 12.Google Scholar
6. Humble, S., Grandma's identity, Math. Gaz. 88 (November 2004) pp. 524–525.Google Scholar
7. Ahlfors, L. V., Complex analysis (2nd edition), McGraw-Hill (1966) p. 159, p. 205.Google Scholar
8. Rudin, W., Real and complex analysis (2nd edition), McGraw-Hill (1974) pp. 330–331.Google Scholar
9. The Euler Archive, http://www.eulerarchive.org Google Scholar
10. Ayoub, R., Euler and the zeta function, Amer. Math. Monthly 81 (1974) pp.1067–1086.Google Scholar
11. Moran, P. A. P., An introduction to probability theory, Oxford University Press (1984) pp.19–21.Google Scholar
12. Bailey, D. H. and Borwein, J. M., Exploratory experimentation and computation, Notices of the AMS 58 (November 2011) pp. 1410–1419. [Available on-line from http://www.ams.orglhome/page.]Google Scholar
13. Russell, D. C., Another Eulerian-type proof, Math. Mag. 64 (1991) p.349.Google Scholar