Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-20T03:40:24.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Using double integrals to solve single integrals

Published online by Cambridge University Press:  14 June 2016

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
Dept. of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Consider the integral

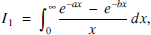
where b > a > 0. First, let us clarify why it even exists. Of course, convergence at infinity is ensured by the exponential terms, but the integrals of and e–ax/x and e–bx/x, taken separately, are divergent at 0, since these integrands equate asymptotically to 1/x as x → 0. However,

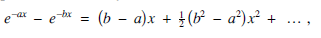
so (e–ax – e–bx)/x tends to the finite limit b – a as x → 0 and there is no problem integrating it on intervals of the form [0, r].

A neat way to evaluate I1 starts by expressing the integrand itself as an integral:

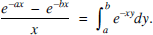(1)

Inserting this into I1 converts it into a double integral.

Type
Research Article
Information
The Mathematical Gazette , Volume 100 , Issue 548 , July 2016 , pp. 257 - 265
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ferrar, W. L., Integral calculus, Oxford University Press (1958).Google Scholar
2.Jameson, G. J. O., Sine, cosine and exponential integrals, Math. Gaz. 99 (July 2015) pp. 276–289.CrossRefGoogle Scholar
3.Hardy, G. H., The integral , Math. Gaz. 5 (June–July 1909) pp. 98–103.CrossRefGoogle Scholar
4. Solution to Problem 95F, Math. Gaz. 96 (March 2012) p. 179.Google Scholar
5.Titchmarsh, E. C., The theory of functions, Oxford University Press (1939).Google Scholar
6.Lord, Nick, Intriguing integrals: an Euler-inspired odyssey, Math. Gaz. 91 (November 2007) pp. 415–427.Google Scholar
7.Walker, P. L., The theory of Fourier series and integrals, John Wiley (1986).Google Scholar
8.Jameson, Graham, Lord, Nick and McKee, James, An inequality for Si (x), Math. Gaz. 99 (March 2015) pp. 133–139.Google Scholar
9.Jameson, G. J. O., Evaluating Fresnel-type integrals, Math. Gaz. 99 (November 2015) pp. 491–498.CrossRefGoogle Scholar