When limnologists (scientists who study lakes) wish to find the volume of a lake they find depth contours, where the depth of the lake is the same at any two points on the given contour. Let A (x) be the area contained in the contour at depth x. The function A (x) is assumed to be strictly decreasing with A (D) = 0 where D is the maximum depth of the lake. The standard formula for the volume that they use is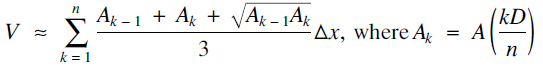

$$V \approx \sum\limits_{k = 1}^n {\frac{{{A_{k - 1}} + {A_k} + \sqrt {{A_k}_{ - 1}{A_k}} }}{2}\Delta x,{\text{ where }}{A_k}{\text{ = }}} A\left( {\frac{{kD}}{n}} \right)$$

over n + 1 equally-spaced depth contours with 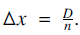$\Delta x{\text{=}}\frac{D}{n}{\text{.}}$ This approach is very well analysed in [1].