Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T18:01:32.283Z Has data issue: false hasContentIssue false
  • English
  • Français

There are only three S•P numbers!

Published online by Cambridge University Press:  01 August 2016

K. Robin McLean
K. Robin McLean*
Affiliation:
Department of Education, PO Box 147, University of Liverpool L69 3BX
Get access Rights & Permissions [Opens in a new window]

Extract

A positive integer, n, which is equal to the sum, S, of its digits multiplied by their product, P, is called an S·P number. S. Parameśwaran gave three examples of such numbers in:

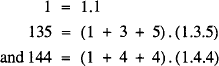
and he conjectured that there are only a finite number of them. This was confirmed when several of us proved that each S·P number has at most 60 digits. There the matter rested for a time. Even if it were possible to test all numbers from 1 to 1060 at the rate of 1040 per second (far beyond the capacity of today’s fastest computer) it would take much longer than the estimated age of the universe to complete the task.

Type
Articles
Information
The Mathematical Gazette , Volume 83 , Issue 496 , March 1999 , pp. 32 - 38
Copyright
Copyright © The Mathematical Association 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)