No CrossRef data available.
Published online by Cambridge University Press: 03 November 2016
1. PSQ is a focal chord of an ellipse and the normals at P and Q intersect at U.
Theorem I. The locus of the foot of the perpendicular from U to PSQ is a similar coaxal conic.
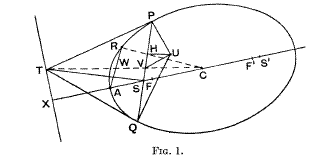
Let the tangents at P and Q meet at T: then T lies on the directrix and TS is perpendicular to PSQ. Draw UH perpendicular to PSQ and AR parallel to PSQ to meet the given conic at R and CVT at W Since TU is the diameter of the circle TQUP, and UH, TS are perpendicular to PQ, V, the mid-point of PQ is also the mid-point of SH But W is the mid-point of AR and hence C, H, R are collinear. Hence CH/CR = CS/CA = e, the eccentricity