Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T23:46:43.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Sums of squares of integers in arithmetic progression

Published online by Cambridge University Press:  23 January 2015

Tom M. Apostol  and
Mamikon A. Mnatsakanian
Tom M. Apostol
Affiliation:
Project MATHEMATICS!, California Institute of Technology, Pasadena, CA 91125 USA
Mamikon A. Mnatsakanian
Affiliation:
Project MATHEMATICS!, California Institute of Technology, Pasadena, CA 91125 USA
Get access Rights & Permissions [Opens in a new window]

Extract

The following striking identities

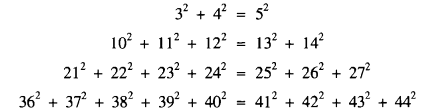
are the cases n = 1,2,3,4 of a remarkable family given by G.J. Dostor [1]:

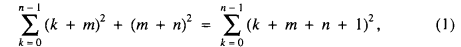
where m = n(2n + 1), and n = 1, 2, … The case m = −n is trivial. If m ≠ −n there are n + 1 squares of consecutive integers on the left and n on the right. We will treat the last term (m + n)2 on the left differently, and refer to it as a transition term relating two sums of squares of n consecutive integers.

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 533 , July 2011 , pp. 186 - 196
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Dostor, G. J., Questions sur les nombres, Archiv der Mathematik und Physik, 64 (1879), pp. 350–352.Google Scholar
2. Dickson, L. E., A history of the theory of numbers, Vol. II (Carnegie Institute, Washington, DC, 1920; reprinted Chelsea Pub., New York, NY, 1952; Dover Pub. Inc., New York, NY, 2005).Google Scholar