Integer linear combinations of cube, fourth, or sixth roots of unity form lattices in the complex plane 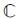. In contrast, integer linear combinations of fifth roots of unity do not form a lattice; in fact, they are dense in 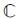. Nevertheless, the geometry for fifth roots of unity has considerable structure. Here we consider only sums of distinct fifth roots of unity, and show that 20 of these sums are orthogonal projections of the vertices of a regular dodecahedron. Pentagonal symmetry here is only to be expected, but it is a little surprising to encounter a plane projection of a polyhedron with much richer dodecahedral symmetry.