Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T18:31:50.891Z Has data issue: false hasContentIssue false
  • English
  • Français

S•P numbers*

Published online by Cambridge University Press:  01 August 2016

A. F. Beardon
A. F. Beardon*
Affiliation:
DPMMS, 16 Mill Lane, Cambridge CB2 1SB, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In a recent issue of the Gazette S. Parameśwaran defined a positive integer n to be an S•P number if it is the product of the sum of its digits and the product of its digits; for example, 135 and 144 are S•P numbers because

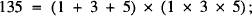
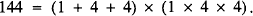
His conjecture that there are only finitely many such numbers was proved in where it was shown that any S•P number is less than 1060. Here, we prove the following result.

Type
Articles
Information
The Mathematical Gazette , Volume 83 , Issue 496 , March 1999 , pp. 25 - 32
Copyright
Copyright © The Mathematical Association 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Editor’s note: Alan Beardon originally submitted a note reducing the upper bound for S•P numbers to 11 billion, and sent a copy to Robin McLean. The two authors then independently completed their proofs, almost simultaneously, using different techniques. I have therefore included both articles.

References

1. Belcher, Paul, Godwin, H.J., Lobb, Andrew, Lord, Nick, McLean, K.Robin and Williams, Phillip, On S P numbers, Math. Gaz. 82 (March 1998) pp.72–75.Google Scholar
2. Parameśwaran, S., Numbers and their digits – a structural pattern, Math. Gaz. 81 (July 1997) p.263.Google Scholar