Article contents
Some Theorems Connected with Maclaurin’s Integral Test
Published online by Cambridge University Press: 03 November 2016
Extract
The theorem of J E. Littlewood stated below includes Maclaurin’s integral test and furnishes the basis for a unified theory of convergence criteria for series of positive terms.
Theorem A. If F(x) is positive monotone decreasing and (Dn) is such that
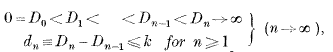
then 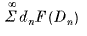 converges or diverges with
converges or diverges with 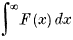 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1939
References
page no 456 note * Note on the convergence of series of positive terms, Messenger of Maths., 39 (1910), 191-2.
page no 456 note † For a discussion of this point of view, vide Rajagopal, C. T., Convergence theorems for series of positive terms, Journ. Indian Math. Soc. (New Series), 3 (1938), 118–125 Google Scholar.
page no 457 note * Bromwich, Infinite Series (1926), 76.
page no 457 note † Theorems connected with Maclaurin’s test for the convergence of series, Proc. Lond. Math. Soc. (2), 9 (1911), 126-144, Ths. 1 and 2.
page no 458 note * The divergence of a complex series is defined by Bromwich (op. cit. 233) as the divergence of the sequence of moduli of the partial sums of the series.
page no 458 note † The particular case Dn=n is proved by Bromwich (op. cit. 235-7) by a method which in principle is not very different from the one employed here.
page no 459 note * It is obvious that this series is convergent for k > 1.
page no 460 note * Math. Gazette, 21 (1937), 161-3.
page no 461 note * It may be noticed that if (Dn
) is any strictly increasing divergent sequence, ![]() a positive decreasing sequenee, the condition
a positive decreasing sequenee, the condition ![]() is necessary for the convergence of Σan
. From this result we can deduce the divergence of
is necessary for the convergence of Σan
. From this result we can deduce the divergence of ![]() by talking
by talking ![]()
page no 22 note † On an integral test of Brink, R. W for the convergence of series, Bull. Amer, Math. Soc. 43 (1937), 405–412, Th. 3Google Scholar.
- 2
- Cited by


