Article contents
Some remarkable integrals derived from a simple algebraic identity
Published online by Cambridge University Press: 23 January 2015
Extract
The identity in question really is simple: it says, for u ≠ −1,
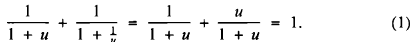
We describe two types of definite integral that look quite formidable, but dissolve into a much simpler form by an application of (1) in a way that seems almost magical.
Both types, or at least special cases of them, have been mathematical folklore for a long time. For example, case (10) below appears in [1, p. 262], published in 1922 (we are grateful to Donald Kershaw for showing us this example). However, they do not seem to figure in most books on calculus except possibly tucked away as an exercise The comprehensive survey [2] mentions the second type on p. 253, but only as a lemma on the way to an identity the authors call the ‘master formula’ We come back to this formula later, but only after describing a number of other more immediate applications.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2013
References
- 1
- Cited by


