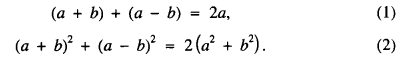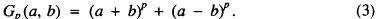Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bakery, Awad A.
2015.
Some Discussions on the Difference Equationxn+1=α+(xn-1m/xnk).
Journal of Function Spaces,
Vol. 2015,
Issue. ,
p.
1.
Jiao, Yutao
Wang, Ping
Niyato, Dusit
Zhao, Jun
Lin, Bin
and
Kim, Dong In
2019.
Task Allocation and Mobile Base Station Deployment in Wireless Powered Spatial Crowdsourcing.
p.
1.
Jiao, Yutao
Wang, Ping
Niyato, Dusit
Lin, Bin
and
Kim, Dong In
2020.
Mechanism Design for Wireless Powered Spatial Crowdsourcing Networks.
IEEE Transactions on Vehicular Technology,
Vol. 69,
Issue. 1,
p.
920.
Zhou, Jing
Claeskens, Gerda
and
Bradic, Jelena
2020.
Detangling robustness in high dimensions: Composite versus model-averaged estimation.
Electronic Journal of Statistics,
Vol. 14,
Issue. 2,
Frassu, Silvia
and
Viglialoro, Giuseppe
2021.
Boundedness in a chemotaxis system with consumed chemoattractant and produced chemorepellent.
Nonlinear Analysis,
Vol. 213,
Issue. ,
p.
112505.
Hadj Taieb, Nizar
2022.
Stability analysis for time-varying nonlinear systems.
International Journal of Control,
Vol. 95,
Issue. 6,
p.
1497.
Jiao, Yutao
Wang, Ping
and
Niyato, Dusit
2022.
Algorithmic Mechanism Design for Internet of Things Services Market.
p.
81.
Columbu, Alessandro
Frassu, Silvia
and
Viglialoro, Giuseppe
2024.
Refined criteria toward boundedness in an attraction–repulsion chemotaxis system with nonlinear productions.
Applicable Analysis,
Vol. 103,
Issue. 2,
p.
415.
Hamzaoui, Abdelfettah
Hadj Taieb, Nizar
and
Hammami, Mohamed Ali
2024.
Practical asymptotic stability for time-varying nonlinear systems.
International Journal of Control,
Vol. 97,
Issue. 12,
p.
2779.
Dandolo, Enrico
Mazzetto, Alessio
Pietracaprina, Andrea
and
Pucci, Geppino
2024.
MapReduce algorithms for robust center-based clustering in doubling metrics.
Journal of Parallel and Distributed Computing,
Vol. 194,
Issue. ,
p.
104966.
Li, Tongxing
Acosta‐Soba, Daniel
Columbu, Alessandro
and
Viglialoro, Giuseppe
2025.
Dissipative Gradient Nonlinearities Prevent δ$\delta$‐Formations in Local and Nonlocal Attraction–Repulsion Chemotaxis Models.
Studies in Applied Mathematics,
Vol. 154,
Issue. 2,
Chargaziya, Georgy
and
Daletskii, Alexei
2025.
Stochastic dynamics of particle systems on unbounded degree graphs.
Journal of Mathematical Physics,
Vol. 66,
Issue. 2,