No CrossRef data available.
Published online by Cambridge University Press: 17 February 2025
The Chebyshev polynomials: some basic facts
The Chebyshev polynomials Tn, named after the Russian mathematician P. L. Chebyshev (1821-1894), are defined by(1)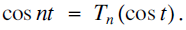 $${\text{cos }}nt = {T_n}({\text{cos }}t).$$
$${\text{cos }}nt = {T_n}({\text{cos }}t).$$