Published online by Cambridge University Press: 15 June 2017
In the performance of digital communication systems over fading channels, the error analysis is typically modelled using a Gaussian probability distribution. One function central to the analysis is what engineers routinely refer to as the (Gaussian) Q-function and is defined by
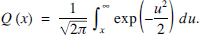 1
1
This is the canonical representation used for the function. In this paper a number of derivations of an important alternative representation for the Q-function known as Craig's formula will be given.