Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T21:42:52.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequences which omit powers

Published online by Cambridge University Press:  01 August 2016

R. D. Nelson
R. D. Nelson*
Affiliation:
Department of Education, University of Manchester, M13 9PL
Get access Rights & Permissions [Opens in a new window]

Extract

Here is an interesting result on sequences amenable to investigation and proof in the classroom. Consider the sequence

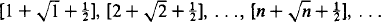
where, as usual, [x] denotes the integer part of x. You will find that you get the sequence

2, 3, 5, 6, 7, 8, 10, . . .

which consists of the natural numbers with the perfect squares omitted. This result is due to H. Halberstam [1] and in this article we verify it and look for generalisations to sequences which omit mth powers.

Type
Research Article
Information
The Mathematical Gazette , Volume 72 , Issue 461 , October 1988 , pp. 208 - 211
Copyright
Copyright © The Mathematical Association 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Halberstam, H., “In praise of arithmetic”, in The teaching of algebra at the pre-college level edited by Braunfield, P. and Deskins, W.E., CEMREL, St. Louis (1975).Google Scholar