Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T16:28:15.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-magic squares and their orthogonal complements

Published online by Cambridge University Press:  01 August 2016

Fernando Mayoral
Fernando Mayoral*
Affiliation:
Depart. de Matemática Aplicada II, E.S, Ingenieros Industrials, Av. Reina Mercedes sin, 41012-Sevilla, Spain
Get access Rights & Permissions [Opens in a new window]

Extract

Not long ago I came across the following quiz in the Sunday supplement of the Spanish newspaper El País: Check that it does not matter how you take any four numbers from the following array; provided that no two of them lie in the same row or column, their sum is always the same.

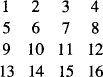
This reminded me of magic squares: square matrices where the sum of the elements in each line (row or column) and diagonal is always the same. Magic squares are a topic in recreational mathematics. Usually one looks for magic squares with elements that are integer, positive and different from each other, e.g. 1,2,…, n2 for a n × n as in

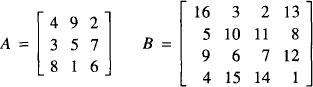
According to a Chinese legend, matrix A appeared engraved on the carapace of a turtle about 2000 BC. On the other hand, matrix B appears in Albrecht Dürer’s engraving Melencholia (1514) [1].

Type
Articles
Information
The Mathematical Gazette , Volume 80 , Issue 488 , July 1996 , pp. 308 - 313
Copyright
Copyright © The Mathematical Association 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andrews, W.S., Magic squares and cubes, Dover, New York (1960).Google Scholar
2. Halmos, P.R., Finite-dimensional Vector Spaces, van Nostrand, Princeton (1958). New edition: Springer-Verlag, Berlin Heidelberg and New York (1974).Google Scholar
3. Strang, G., Introduction to Linear Algebra, Wellesley Cambridge Press, Wellesley MA (1983).Google Scholar
4. Weiner, L.M., The algebra of semi-magic squares, Amer. Math. Monthly 62 (1955) pp. 237–239.Google Scholar
5. den Essen, Arno van, Magic Squares and Linear Algebra, Amer. Math. Monthly 97 (1990) pp. 60–62.CrossRefGoogle Scholar