Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T08:18:09.755Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting the general cubic: a simplification of Cardano's solution

Published online by Cambridge University Press:  11 October 2023

Hsin-Chieh Liao ,
Mark Saul  and
Peter J.-S Shiue
Hsin-Chieh Liao
Affiliation:
Department of Mathematics, University of Miami, Florida 33146, USA e-mail: [email protected]
Mark Saul
Affiliation:
Nine Nine Cultural and Educational Foundation, 9F, No. 300, Sec 3. Roosevelt Road, Zhongzheng Dist., Taipei City 10900, Taiwan e-mail: [email protected]
Peter J.-S Shiue
Affiliation:
Department of Mathematical Sciences, University of Nevada, Las Vegas NV 89154-4020, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a polynomial equation x3 + ax2 + bx + c = 0 of degree 3 with real coefficients, we may translate the variable by replacing x with x − 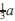to make the quadratic term vanish. We then obtain a simpler equation x3 + px + q = 0 where 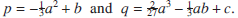Therefore, in order to solve a polynomial equation of degree 3, it is sufficient to solve equations of the form x3 + px + q = 0.

Type
Articles
Information
The Mathematical Gazette , Volume 107 , Issue 570 , November 2023 , pp. 438 - 444
Check for updates
Copyright
© The Authors, 2023 Published by Cambridge University Press on behalf of The Mathematical Association

References

Harris, J. W., Stocker, H., Handbook of mathematics and computational science, Springer-Verlaine (1998).CrossRefGoogle Scholar
Burton, D. M., Abstract algebra, Wm. C. Brown (1988).Google Scholar
Gilbert, L., Gilbert, J., Elementary modern algebra (8th edn), Cengage Learning (2015).Google Scholar
Sylvester, J. J., On a remarkable discovery in the theory of canonical forms and of hyperdeterminants, Math. Mag. 2 (1851) pp. 391–410.Google Scholar
Chen, W.Y.C., Cubic equations through the looking glass of Sylvester, College Math. J., 53(5) (2022) pp. 396–398.CrossRefGoogle Scholar
Liao, H. C., Shiue, P. J. -S, Cubic equations revisited (in Chinese), Math Media, 46(1) (2022) pp. 33–39.Google Scholar