Finding an expression for the length of a curve is one of the simpler geometric applications of the integral. If f is a function with a continuous derivative, then the expression 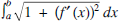gives the length of the curve y = f (x) on an interval [a, b]. However, after writing out the integrand for familiar functions such as y = x2 and y = sin x, it quickly becomes apparent that, in general, finding an antiderivative is a challenge. Of course, a computer can give accurate approximations for the value of the integral for the length of a curve, but it would be nice to find the exact length rather than a decimal approximation. In his work on geometry (from 1637), Descartes stated that he believed it was not possible to determine the exact lengths of curves. However, just twenty years later, William Neile was able to find the length of arcs of semicubical parabolas (see Katz [1]). These curves have the form y = kx3/2 and are usually the first examples or exercises given to students since the resulting integral is very easy to compute. In this paper, we are going to examine this curve and other related curves and consider problems such as the following: find rational numbers a and b so that the length of the curve over the interval is an [a, b] integer. As we shall see, problems such as this provide a variety of opportunities for undergraduate students to explore some interesting mathematics arising from a few simple and accessible questions.