Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T06:05:57.776Z Has data issue: false hasContentIssue false
  • English
  • Français

The probabilistic nature of Wallis's formula

Published online by Cambridge University Press:  23 January 2015

Rasul A. Khan
Get access Rights & Permissions [Opens in a new window]

Extract

The beautiful representation of π by Wallis's product formula has attracted many authors who have given a variety of proofs (see [1, 2, 3, 4, 5, 6, 7]). The purpose of this note is to revisit some elementary derivations with a focus on probabilistic/statistical flavours of this formula. The famous Wallis's product formula for 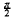is given by

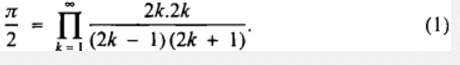
There are a number proofs available for this formula scattered in the literature. Here we will concentrate on the probabilistic nature of this formula.

Type
Articles
Information
The Mathematical Gazette , Volume 96 , Issue 536 , July 2012 , pp. 193 - 200
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Boros, G. and Moll, V., Irresistible integrals, symbolics, analysis and experiments in the evaluation of integrals, Cambridge University Press, (2004).CrossRefGoogle Scholar
2. Courant, R., Differential and integral calculus, Vol. I, Wiley, New York (1968).Google Scholar
3. Courant, R., Differential and integral calculus, Vol. II, Wiley, New York (1968).Google Scholar
4. Gurland, J., On Wallis' formula, Amer. Math. Monthly 63 (1956) pp. 643–645.Google Scholar
5. Miller, Steven J., A probabilistic proof of Wallis's formula for π, Amer. Math. Monthly 115 no. 8 (2008) pp. 740–745.CrossRefGoogle Scholar
6. Vito, Lampret, Wallis sequence estimated through the Euler-Maclaurin formula, Austral. Math. Soc. Gaz. 31, no. 5 (2004) pp. 328–339.Google Scholar
7. Widder, David V., Advanced calculus, Prentice Hall (1947), p. 311.Google Scholar
8. Levrie, Paul and Daems, Walter, Evaluating the probability integral using Wallis's product formula for π, Amer. Math. Monthly 116, no. 6 (2009) pp. 538–541.CrossRefGoogle Scholar
9. Cramer, H., Mathematical methods of statistics, Princeton University Press (1946).Google Scholar