No CrossRef data available.
Published online by Cambridge University Press: 15 February 2024
The 2 × 2 identity matrix, 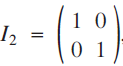 $${I_2} = \left( \begin{gathered}{\rm{1 \,\,\,0}} \hfill \\{\rm{0 \,\,\,1}} \hfill \\ \end{gathered}\right)$$, has an infinite number of square roots. The purpose of this paper is to show some interesting patterns that appear among these square roots. In the process, we will take a brief tour of some topics in number theory, including Pythagorean triples, Eisenstein triples, Fibonacci numbers, Pell numbers and Diophantine triples.
$${I_2} = \left( \begin{gathered}{\rm{1 \,\,\,0}} \hfill \\{\rm{0 \,\,\,1}} \hfill \\ \end{gathered}\right)$$, has an infinite number of square roots. The purpose of this paper is to show some interesting patterns that appear among these square roots. In the process, we will take a brief tour of some topics in number theory, including Pythagorean triples, Eisenstein triples, Fibonacci numbers, Pell numbers and Diophantine triples.