Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T14:25:54.981Z Has data issue: false hasContentIssue false
  • English
  • Français

The Oriental Influence on Greek Mathematics

Published online by Cambridge University Press:  03 November 2016

R.J. Gillings
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of finding rational integral numbers which could be made the sides of right triangles, is said by Proclus to have been solved by Pythagoras, by a method which is equivalent to the use of the formula,

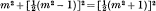
where m is any odd integer.

Heath (1) quotes Proclus’ statement as follows:

“The method starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it takes the square of it, subtracts unity, and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side the hypotenuse.”

Type
Research Article
Information
The Mathematical Gazette , Volume 39 , Issue 329 , September 1955 , pp. 187 - 190
Copyright
Copyright © The Mathematical Association 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1) Heath, SirThomas, L., The Thirteen Books of Euclid’s Elements. Second edition. Cambridge University Press. 1926, Vol. 1, p. 356.Google Scholar
(2) Coolidge, J.L., The Mathematics of Great Amateurs. Oxford University Press. 1949, p.59 and p.16.Google Scholar
(3) Neugebauer, 0., The Exact Sciences in Antiquity. Ejnar Munksguard. Copenhagen, 1951, p. 52.Google Scholar
(4) Gillings, R.J., Unexplained Error in Babylonian Cuneiform Tablet, Plimpton 322. The Australian Journal of Science, Vol. 16, No. 2. October 1953, p. 54.Google Scholar