Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T14:48:46.804Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Intersections of a Central Conic and its Principal Hyperbolas

Published online by Cambridge University Press:  03 November 2016

C. T. Rajagopal
Get access Rights & Permissions [Opens in a new window]

Extract

Let an ellipse or a hyperbola be given by the equation

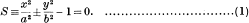
Then, following Vaidyanathaswamy [8, p. 124], we shall refer to a hyperbola H having its asymptotes parallel to the principal axes of S as a principal hyperbola of S. H is thus given by an equation of the type

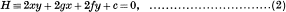
and it is uniquely determined when we know three of its intersections with S. It is one of the purposes of this article to bring together some of the elementary properties of H which have been ignored, quite unjustifiably, by most of the textbooks on conic sections produced after Casey's Analytical Geometry [2]. Another purpose which it is hoped the article will serve is that of bringing within easy reach of students, who have had only a preliminary course in geometries of two and three dimensions, some of Vaidyanathaswamy's investigations into the concurrency of normals to a central conic [6].

Type
Research Article
Information
The Mathematical Gazette , Volume 35 , Issue 312 , May 1951 , pp. 97 - 104
Copyright
Copyright © The Mathematical Association 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baker, H. F., Introduction to Plane Geometry (1943).Google Scholar
2. Casey, J., Treatise on Analytical Geometry (1893).Google Scholar
3. Hamflett, W. G., “Joachimsthal’s theorem,” Math. Gazette, vol. 32 (1948), pp. 86–7.Google Scholar
4. Krishnaswami Ayyangar, A. A., “Conormal points on an ellipse,” Math. Gazette, vol. 18 (1934), p. 324.Google Scholar
5. Vaidyanathaswamy, R., “On Burnside’s condition for the concurrence of three normals to a conic,“ Journal Indian Math. Soc. (Notes and Questions), vol. 18 (1930), pp. 207–8.Google Scholar
6. Vaidyanathaswamy, R., “On the feet of concurrent normals of a conic,” Journal Indian Math. Soc., vol. 18 (1930), pp. 296–312.Google Scholar
7. Vaidyanathaswamy, R., “On the quasi-normals of a central conic,” Journal Indian Math. Soc. (Notes and Questions), vol. 18 (1930), pp. 281–9.Google Scholar
8. Vaidyanathaswamy, R., “On the 0-normals of a conic,” Math. Student, vol. 2 (1933), pp. 121–130.Google Scholar