Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T21:26:48.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Diophantine equation

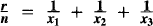
Published online by Cambridge University Press:  01 August 2016

Clotilde Luz Clifton-Everest
Clotilde Luz Clifton-Everest*
Affiliation:
186 Gilbert Road, Cambridge CB4 3PB, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this article we discuss two main theorems relating to two different decompositions of the fraction r/n as a sum of three fractions of numerator one. Each decomposition is associated with three positive integers a, b, m such that m is a divisor of an + b. Through this discussion we devise a procedure to find values of a, b and m for a given n.

Type
Articles
Information
The Mathematical Gazette , Volume 91 , Issue 522 , November 2007 , pp. 481 - 492
Copyright
Copyright © The Mathematical Association 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Erdős, P. and Graham, R.L. Old and new problems and results in combinatorial number theory, Monographies de L’Enseignement Mathématique de Genève 28 (1980) pp. 30–44.Google Scholar
2. Guy, R. K. Unsolved problems in number theory, Springer-Verlag (1981) pp. 87–93.Google Scholar
3. Clifton-Everest, C. Luz Fracçôes Egipcias, Bol. Soc. Port. Mat. 50 (May 2004) pp. 45–78.Google Scholar
4. Clifton-Everest, C. Luz Errata ao meu artigo “Fracçôes Egipcias”, Bol. Soc. Port. Mat. 51 (October 2004) p. 47.Google Scholar
5. Mordell, L. J. Diophantine equations, Academic Press (1969) pp. 287–290.Google Scholar
6. Webb, W. A. Rationals not expressible as a sum of three unit fractions, Elemente der Mathematik 29 (1974) pp. 1–6.Google Scholar
7. Sierpinski, W. Elementary theory of numbers, Monografie Matematyczne 42, Warszawa (1964).Google Scholar
8. Obláth, R. Sur l’équation diophantienne 4/n = 1/x 1 + 1/x 2 + 1/x 3 , Mathesis 59 (1950) pp. 308–316.Google Scholar