Several writers have studied algebras in which multiplication is non-associative, that is, x yz≠xy z. It is necessary in a non-associative algebra to distinguish the possible interpretations of a power xn In a non-commutative non-associative algebra x2 is unique, x3 can mean xx2 or x2x; x4 can mean x xx2, x x2x, x2x2, xx2x or x2x x, x5 has 14 interpretations; x6 has 42; and so on. In a commutative non-associative algebra, the possible interpretations are fewer x3 is unique, x4 can mean xx3 or x2x2, x5 can mean x xx3, x x2x2 or x2x3, x6 has 6 interpretations, and so on. The problem considered here is how many meanings are there for xn (A) in a general non-commutative non-associative algebra ? (B) in a general commutative non-associative algebra ? The answer to (A) is 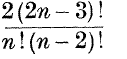I am not able to find any such simple formula for (B).