No CrossRef data available.
Article contents
The Methods of Integration of the Differential Equation: P dx + Q dy + R dz=0
Published online by Cambridge University Press: 03 November 2016
Extract
In this article an attempt has been made to indicate the ordinary methods of integration of the total differential equation
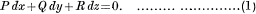
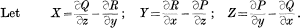
Then the condition for integrability of (1) , i.e, the condition that (1) may possess a single integral equivalent of the form ϕ(x, y, z)= c, is
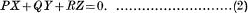
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mathematical Association 1933
References
page 105 of note * References are to pages in the undermentioned works, and are abbreviated as follows : B. : Boole, G. Differential Equatzons, 4th ed. (1877).Google Scholar FI : Forsgth, A.R., Treatise on Differential Eqzirttzons, 6th ed. (1929).Google Scholar I .: Forsvth, A.R.. Theory of Differential Enuatlons. Part I (1890).Google Scholar G. : Goursag Cows, E. l. 11, 4th ed. (1925).Google Scholar I. : Ince, E.L., Ordinary Dzfferentinl Equations (1927).Google Scholar P : Piaggio, H.T.H., Treatise on Differential Equations, revised ed. (1825).Google Scholar W : Wilson, E.B., Advanced Calculus (1911).Google Scholar
page 108 of note * See also the footnote to section VI.
page 109 of note * Though not usually desirable as a practical method of integration, after λ has been found, instead of proceeding to the final integration, this method may be used in conjunction with method IV Thus, if µ and µ, have the values given in IV (ii). the above integral may be written in either of the forms
![]()
- 1
- Cited by


